Refraction through lens
Selina ICSE Solutions for Class 10 Physics Chapter 5 Refraction through Lens
Exercise 5(A)
Solution 1.
A lens is a transparent refracting medium bounded by two curved surfaces which are generally spherical.
Solution 2.
Solution 3.
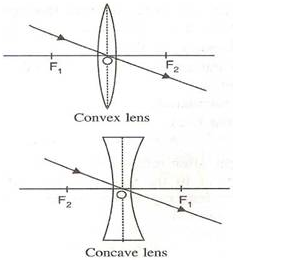
Convex lens:
- It converge the incident rays towards the principal axis.
- It has a real focus.
Concave lens:
- It diverges the incident rays away from the principal axis.
- It has a virtual focus.
Solution 4.
Equiconvex lens is converging.
Solution 5.
Concave lens will show the divergent action on a light beam.
Solution 6.
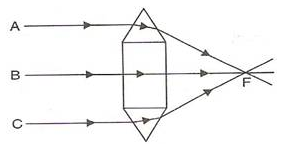
As shown in the figure the convex lens has two glass prisms and one glass block. One of the glass prisms is situated above the glass block and one below the block.
Solution 7.
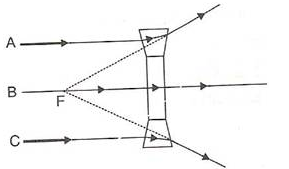
As shown in the figure the concave lens has two glass prisms and one glass block. One of the glass prisms is situated above the glass block and one below the block.
Solution 8.
If a parallel beam of light is incident on a convex lens then the upper part of the lens bends the incident ray downwards. The lower part bens the ray upwards while the central part passes the ray undeviated.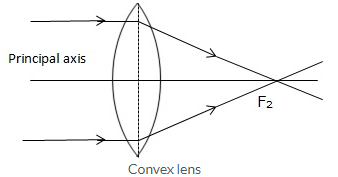
But in case of a concave lens the upper part of the lens bends the incident ray upwards and lower part bends the ray downwards while the central part passes the ray undeviated.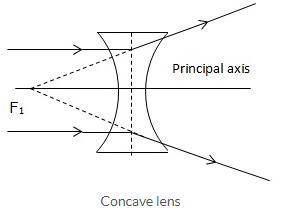
Solution 9.
It is the line joining the centers of curvature of the two surfaces of the lens.
Solution 10.
It is point on the principal axis of the lens such that a ray of light passing through this point emerges parallel to its direction of incidence.
It is marked by letter O in the figure. The optical centre is thus the centre of the lens.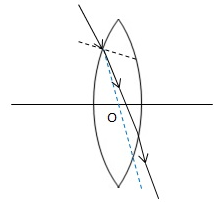
Solution 11.

Solution 12.
A lens is called an equiconvex or equiconcave when radii of curvature of the two surfaces of lens are equal.
Solution 13.
A light ray can pass through a lens from either direction. Therefore, a lens has two principal foci.
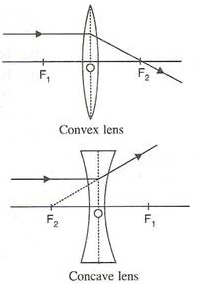
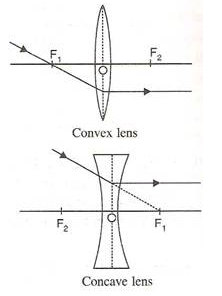
For a convex lens, the first focal point is a point F1 on the principal axis of the lens such that the rays of light starting from it or passing through it, after refraction through lens, become parallel to the principal axis of the lens.
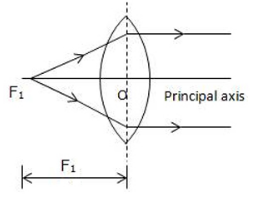
The second focal point for a convex lens is a point F2 on the principal axis such that the rays of light incident parallel to the principal axis, after refraction from the lens, pass through it.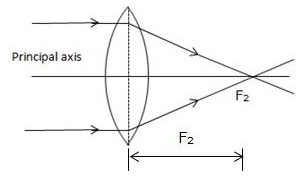
Solution 14.
A light ray can pass through a lens from either direction. Therefore, a lens has two principal foci.
For a concave lens, the first focal point is a point F1 on the principal axis of the lens such that the incident rays of light appearing to meet at it, after refraction from the lens become parallel to the principal axis of the lens.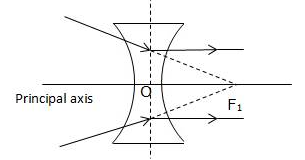
The second focal point for a concave lens is a point F2 on the principal axis of the lens such that the rays of light incident parallel to the principal axis, after refraction from the lens, appear to be diverging from this point.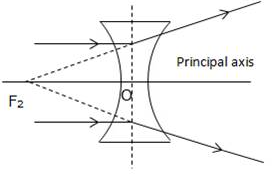
Solution 15.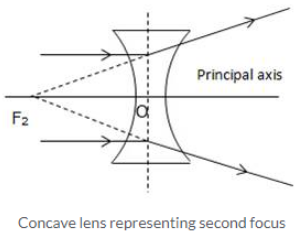
Solution 16.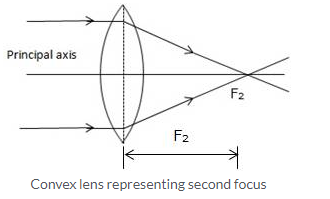
Solution 17.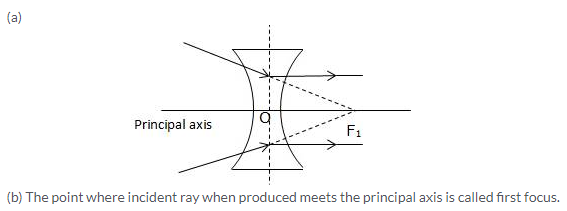
Solution 18.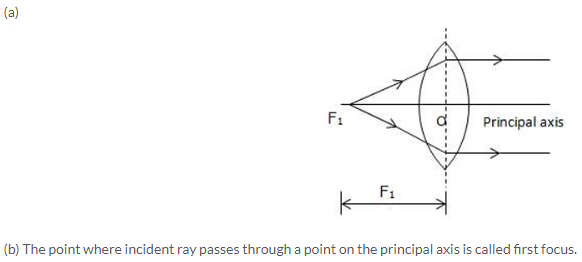
Solution 19.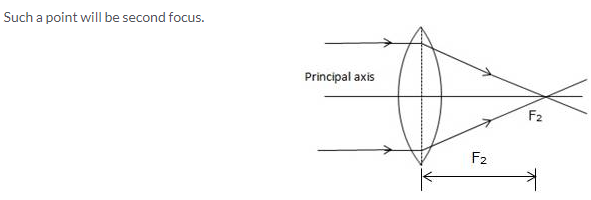
Solution 20.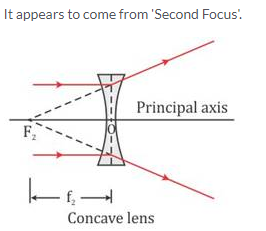
Solution 21.
The distance from the optical centre O of the lens to its second focal point is called the focal length of the lens.
Solution 22.
A plane passing through the focal point and normal to the principal axis of the lens is called the first focal plane.
Solution 23.
(i) If a lens has both its focal length equal medium is same on either side of lens.
(ii)If a ray passes undeviated through the lens it is incident at the optical centre of the lens.
Solution 24.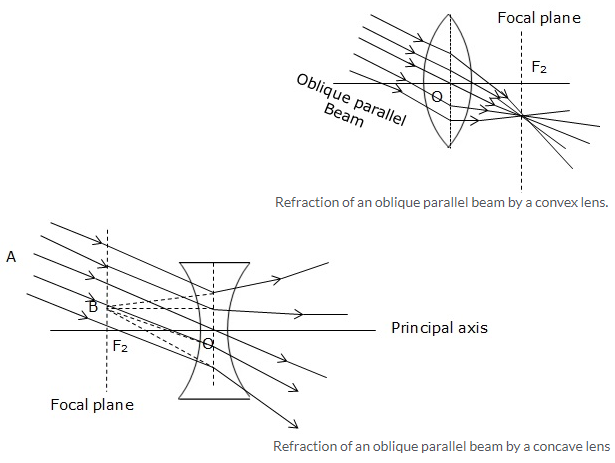
Solution 25.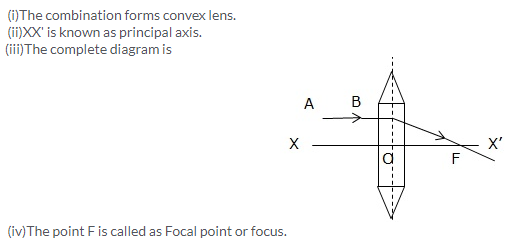
Solution 26.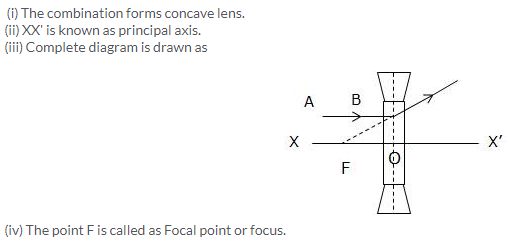
Solution 27.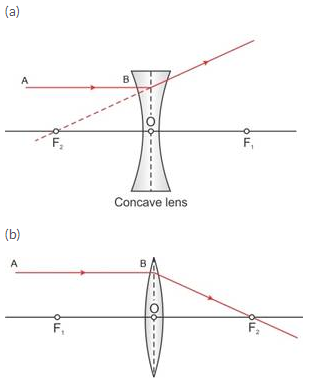
Solution 28.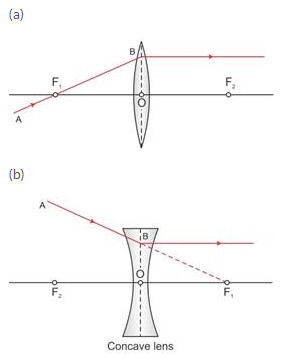
Solution 29.
(a) If half part of a convex lens is covered, the focal length does not change, but the intensity of image decreases.
(b) A convex lens is placed in water. Its focal length will increase.
(c) The focal length of a thin convex lens is more than that of a thick convex lens.
Solution 1 (MCQ).
First focus
Solution 2 (MCQ).
Its second focus
Exercise 5(B)
Solution 1.
- A ray of light incident at the optical centre O of the lens passes undeviated through the lens.
- A ray of light incident parallel to the principal axis of the lens, after refraction passes through the second focus F2 (in a convex lens) or appears to come from the second focus F2 (in a concave lens).
- A ray of light passing through the first focus F1 (in a convex lens) or directed towards the first focus F1 (in a concave lens), emerges parallel to the principal axis after refraction.
Solution 2.
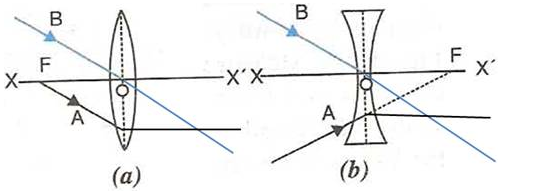
Solution 3.
| Real image | Virtual image |
| 1. A real image is formed due to actual intersection of refracted (or reflected) rays. | 1. A virtual image is formed when the refracted (or reflected) rays meet if they are produced backwards. |
| 2. A real image can be obtained on a screen. | 2. A virtual image can not be obtained on a screen. |
| 3. A real image is inverted with respect to the object. | 3. A virtual image is erect with respect to the object. |
Solution 4.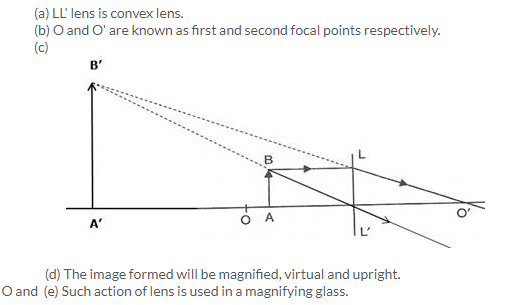
Solution 5.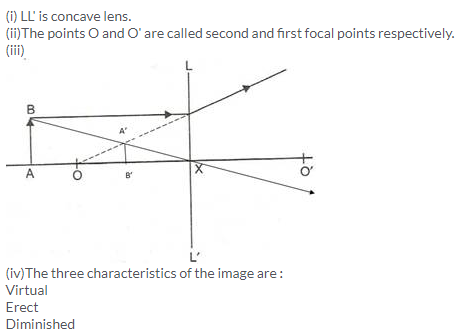
Solution 6.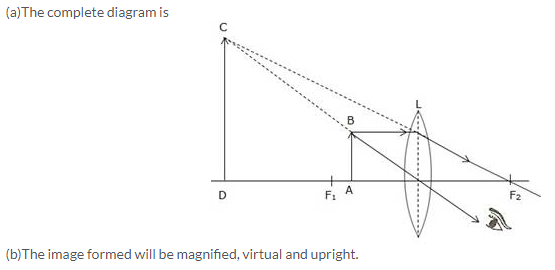
Solution 7.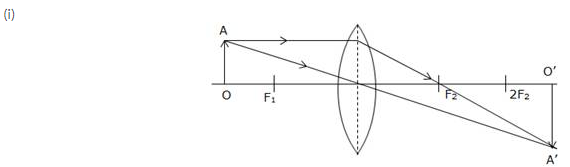
(ii) The position of the images will be more than twice the focal length of lens.
(iii) The image will be magnified, real and inverted.
(iv) As the object move towards F1 the image will shift away from F2 and it is magnified. At F1 the image will form at infinity and it is highly magnified. Between F1 and optical centre, the image will form on the same side of object and will be magnified.
Solution 8.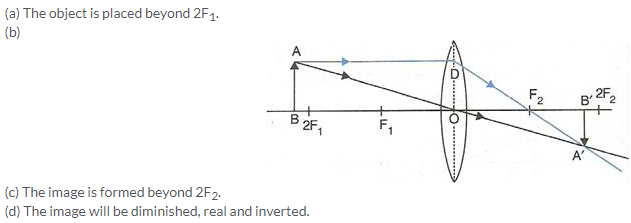
Solution 9.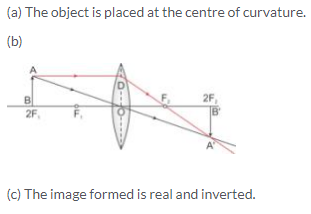
Solution 10.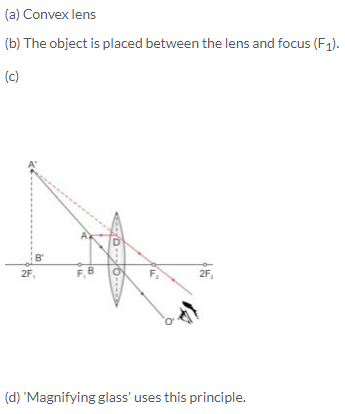
Solution 13.
Let the candle is placed beyond 2F1 and its diminished image which is real and inverted is formed between F2 and 2F2.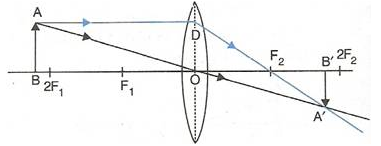
Here the candle is AB and its real and inverted image is formed between F2 and 2F2.
Solution 14.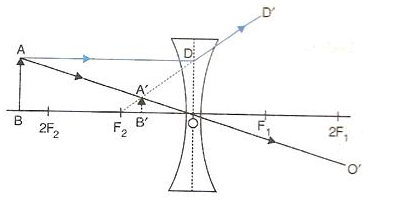
Solution 15.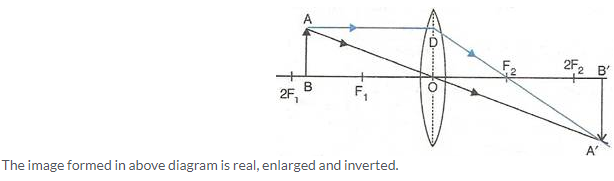
Solution 16.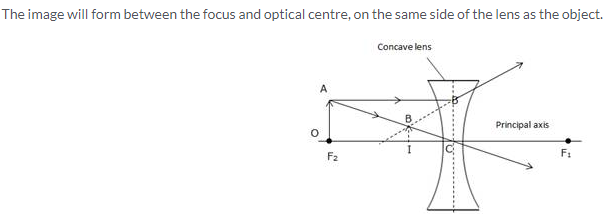
Solution 17.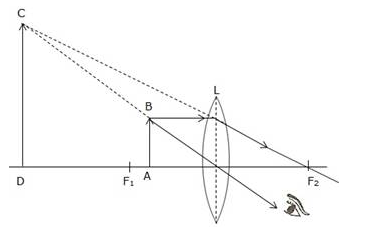
The object is placed between focal point F1 and convex lens and its image is formed at the same side of the lens which is enlarged.
So this lens can be used as a magnifying lens.
Solution 18.
The sun is at infinity so convex lens forms its image at second focal point which is real and very much diminished in size.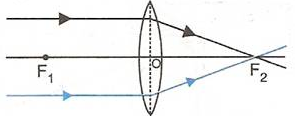
While using the convex lens as burning glass, the rays of light from the sun (at infinity) are brought to focus on a piece of paper kept at the second focal plane of the lens. Due to sufficient heat of the sun rays, the paper burns. Hence this lens is termed as ‘burning glass’.
Solution 19.
(a) This is convex lens.
(b) The nature of the image is real.
Solution 20.
(a) Convex lens.
(b) Virtual.
Solution 21.
(a) Concave lens
(b) Image is diminished
Solution 23.
Image formed by a concave lens is virtual and diminished.
Solution 24.
The virtual image formed by a convex lens will be magnified and upright.
Solution 25.
(a) at focus,
(b) at 2F,
(c) between F and 2F,
(d) between optical centre and focus.
Solution 26.
| Type of lens | Position of object | Nature of image | Size of image |
| Convex | Between optic centre and focus | Virtual and upright | Magnified |
| Convex | At focus | Real and inverted | Very much magnified |
| Concave | At infinity | Virtual and upright | Highly diminished |
| Concave | At any distance | Virtual and upright | Diminished |
Solution 27.
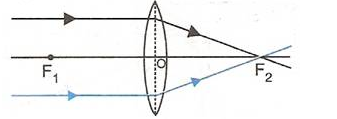
- When the object is situated at infinity, the position of image is at F2, it is very much diminished in size and it is real and inverted.
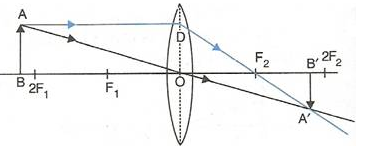
- When the object (AB) is situated beyond 2F1, the position of image (A’B’) is between F2 and 2F2, it is diminished in size and real and inverted.
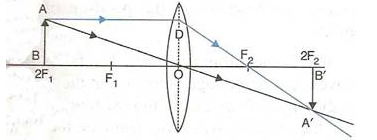
- When the object (AB) is situated at 2F1, the position of image (A’B’) is at 2F2, it is of same size as the object and real and inverted.
- When the object (AB) is situated between 2F1and F1, the position of image (A’B’) is beyond 2F2, it is magnified in size and real and inverted.
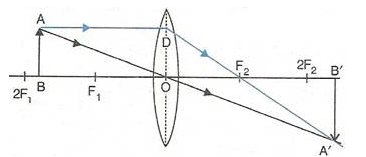
- When the object (AB) is situated at F1, the position of image is at infinity; it is very much magnified in size and real and inverted.
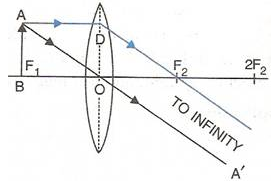
- When the object (AB) is situated between lens and F1, the position of image (CD) is on the same side, behind the object; it is magnified in size and virtual and upright.
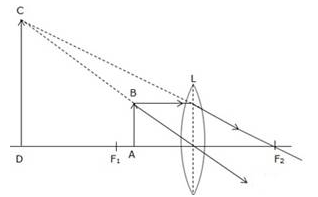
Solution 28.
- When object (AB) is situated at infinity then parallel rays from object appears to fall on concave lens. Due to which image forms at focus. This image is highly diminished in size and virtual and upright.
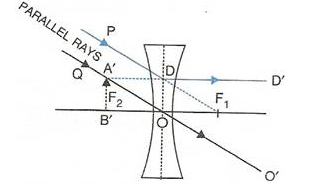
- When object (AB) is situated at any point between infinity and optical centre of the lens then image forms between focus and optical centre. This image is diminished in size and virtual and upright.
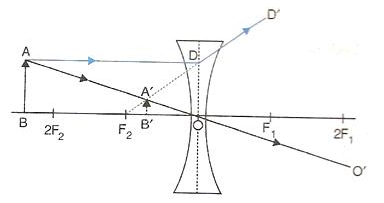
Solution 29.
(a) An object is placed at a distance of more than 40 cm from a convex lens of focal length 20 cm. The image formed is real, inverted and diminished.
(b) An object is placed at a distance 2f from a convex lens of focal length f. The image formed is equal to that of the object.
(c) An object is placed at a distance 5 cm from a convex lens of focal length 10 cm. The image formed is virtual, upright and magnified.
Solution 30.
(a) False
(b) False
(c) False
(d) True
(e) False
Solution 1 (MCQ).
The focal length of the convex lens is 10 cm.
Hint: As the object distance = image distance, the object must be kept at 2f.
Therefore, 2f = 20 cm or f = 10 cm.
Solution 2 (MCQ).
Virtual and enlarged.
Explanation: When the object is kept between optical centre and focus of a convex lens, the image is formed on the same side, behind the object. The image thus formed is virtual, enlarged and erect.
Solution 3 (MCQ).
Virtual, upright and diminished
Hint: Concave lens forms virtual, upright and diminished image for all positions of the object.
Exercise 5(C)
Solution 1.
- The axis along which the distances are measured is called as the principal axis. These distances are measured from the optical centre of the lens.
- All the distances which are measured along the direction of the incident ray of the light are taken positive, while the distances opposite to the direction of the incident ray are taken as negative.
- All the lengths that are measured above the principal axis are taken positive, while the length below the principal axis is considered negative.
- The focal length of the convex lens is taken positive and that of concave lens is negative.
Solution 1 (MCQ).
Magnification is -0.5. The negative sign of magnification indicates that the image is real while 0.5 indicates that the image is diminished. A convex lens only forms a real and diminished image of an object. Hence, the correct answer is option (d).
Solution 2.
(i) The positive focal length of a lens indicates that it is a convex lens.
(ii) The negative focal length of a lens indicates that it is a concave lens.
Solution 3.
Lens formula:![]()
- The distance of the object from the optical centre is called the object distance (u).
- The distance of the image from the optical centre is called the image distance (v).
- The distance of the principal focus from the optical centre is called the focal length (f).
Solution 3 (MCQ).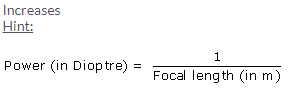
Solution 4.
The term magnification means a comparison between the size of the image formed by a lens with respect to the size of the object.
For a lens: Magnification ‘m’ is the ratio of the height of the image to the height of the object.
Solution 4 MCQ.
Power of a lens is +1.0 D. The positive sign indicates that the focal length of the lens is positive which indicates the lens is a convex lens.

Solution 5.
(i) Positive sign of magnification indicates that the image is virtual while negative sign indicates that the image is real.
(ii) Positive sign of magnification indicates that the image is erect while negative sign indicates that the image is inverted.
Solution 6.
The power of a lens is a measure of deviation produced by it in the path of rays refracted through it.
Its unit is Dioptre (D).
Solution 7.![]()
Solution 8.
If focal length of a lens doubled then its power gets halved.
Solution 9.
The sign of power depends on the direction in which a light ray is deviated by the lens. The power could be positive or negative. If a lens deviates a ray towards its centre (converges), the power is positive and if it deviates the ray away from its centre (diverges), the power is negative.
Solution 10.
It is a concave.
Solution 9 (MCQ).
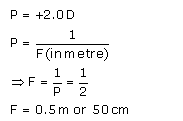
Solution 10 (MCQ).
Solution 1 (Num).
Solution 2 (Num).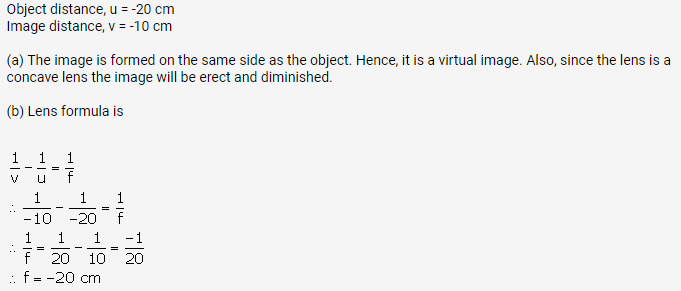
Solution 3 (Num).
Solution 4 (Num).
Solution 5 (Num).
Solution 6 (Num).
Solution 7 (Num).
Solution 8 (Num).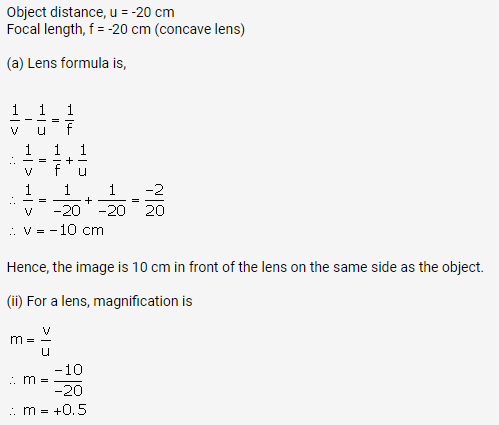
Solution 9 (Num).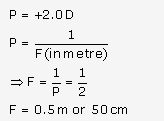
Solution 10 (Num).
Solution 11 (Num).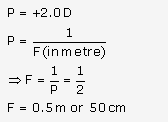
Solution 11 (Num).
Solution 13 (Num).
Exercise 5(D)
Solution 1.
Magnifying glass is a convex lens of short focal length. It is mounted in a lens holder for practical use.
It is used to see and read the small letters and figures. It is used by watch makers to see the small parts and screws of the watch.
Solution 2.
Let the object (AB) is situated between focal length and optical centre of a convex lens then its image (A’B’) will form on the same side of lens.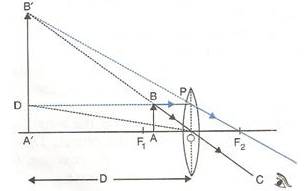
The image formed will be virtual, magnified and erect.
Solution 3.
The object is placed between the lens and principal focus.
The image is obtained between the lens and principal focus.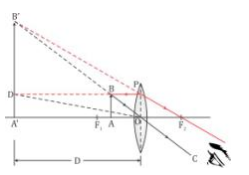
Solution 4.
The magnifying power of the microscope is defined as the ratio of the angle subtended by the image at the eye to the angle subtended by the object (assumed to be placed at the least distance of distinct vision D = 25 cm) at the eye, i.e.,![]()
where F is the focal length of the lens.
The magnifying power of a microscope can be increased by using the lens of short focal length. But it cannot be increased indefinitely.
Solution 5.
The two applications of a convex lens are:-
- It is used as an objective lens in a telescope, camera, slide projector, etc.
- With its short focal length it is also used as a magnifying glass.
The two applications of a concave lens are:-
- A person suffering from short sightedness or myopia wears spectacles having concave lens.
- A concave lens is used as eye lens in a Galilean telescope to obtain an erect final image of the object.
Solution 6.
The approximate focal length of a convex lens can be determined by using the principle that a beam of parallel rays incident from a distant object is converged in the focal plane of the lens.
In an open space, against a white wall, a metre scale is placed horizontally with its 0 cm end touching the wall.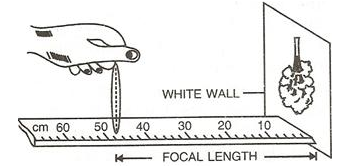
By moving the convex lens to and fro along the scale, focus a distant object on wall. The image which forms on the wall is very near to the focus of the lens and the distance of the lens from the image is read directly by the metre scale. This gives the approximate focal length of the lens.
Solution 7.
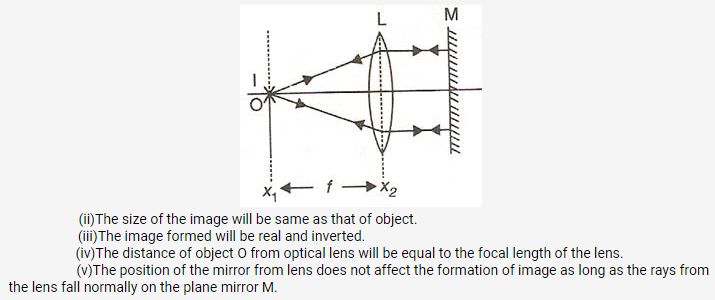
Solution 8.
To determine focal length by using plane mirror we need a vertical stand, a plane mirror, a lens and a pin.
Place the lens L on a plane mirror MM’ horizontally. Arrange a pin P on the clamp of a vertical stand such that the tip of pin is vertically above the centre O of the lens.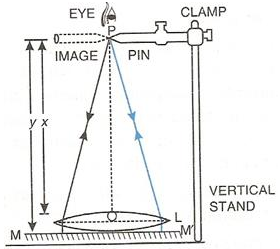
Adjust the height of the pin until it has no parallax (i.e., when the pin and its image shift together) with its inverted image as seen from vertically above the pin.
Now measure the distance x of the pin from the lens and the distance y of the pin from the mirror, using a metre scale and a plumb line. Calculate the average of the two distances. This gives the focal length of the lens, i.e.,![]()
Comments
Post a Comment